 01八大排序
01八大排序
# 01 八大排序
虽然在刷题中我们可以使用高级编程语言提供封装好的排序算法便捷实现排序任务,例如 C++ 里可以通过 STL 中基于快速排序实现的 std::sort() 算法便捷实现排序任务。而且刷题时除非题目考点就是排序算法,否则也不建议自己手写排序算法。
但是知识都是有着累积发展的过程,我们熟习各种基础的排序算法可以加深自己对算法的基本理解;同时我们也可以基于对基础排序算法的理解,快速解出由这些排序算法引申出来的题目。
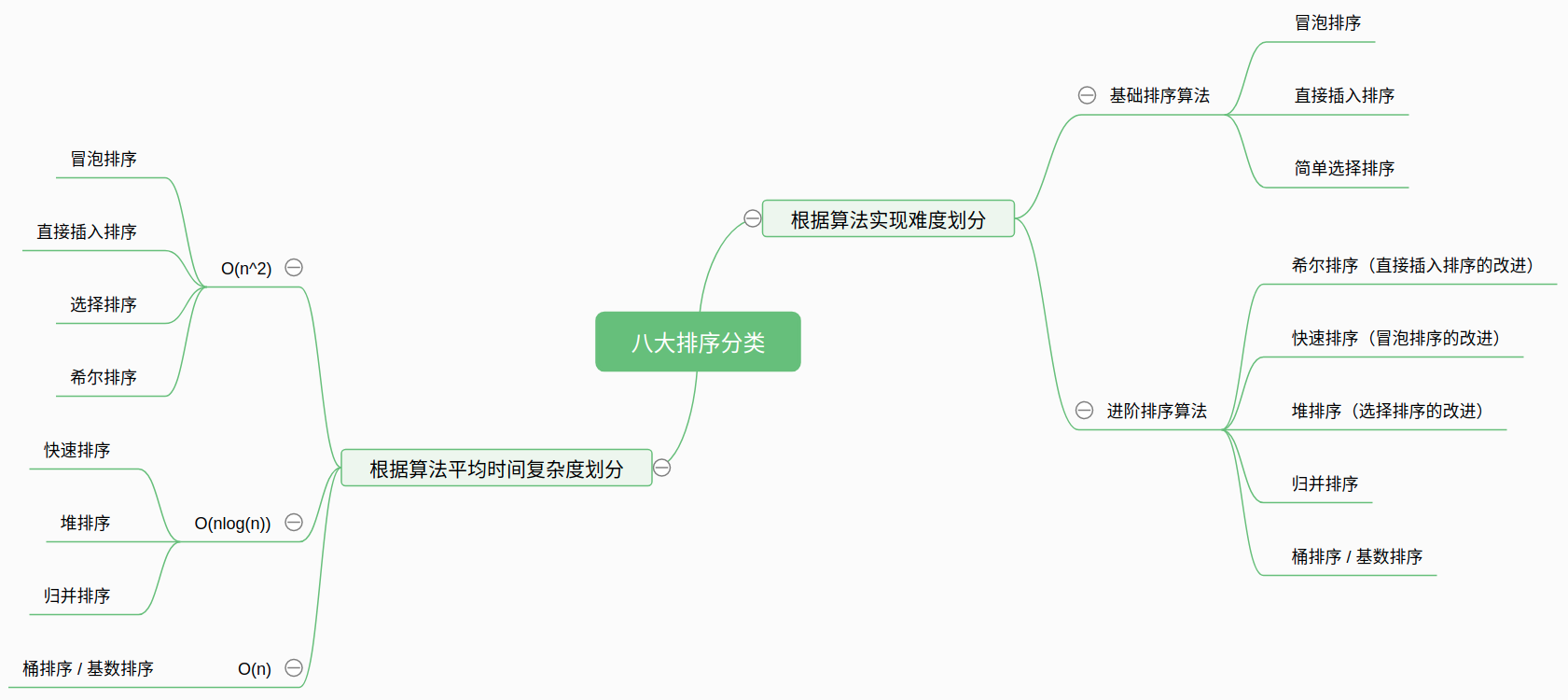
八大排序算法有着不同的实现思想,他们实现的时间复杂度也有所差异,根据不同的时间复杂度和算法稳定性他们有着不同的应用场景:
快速排序、堆排序和归并排序具有较好的算法效率,其中快速排序性能最好但是算法不稳定,堆排序不需要额外的空间开销,而归并排序是稳定性较高的算法但是需要较大空间开销。
在排序数据量较小的情况下,可以根据元素分布是否有序选择使用直接插入排序或者简单选择排序,他们也能够提供稳定且较高的算法性能。一般不使用冒泡排序,其性能相交于其他算法较差。
桶排序/基数排序是一种稳定的算法且具有较好算法性能,但是该算法的使用存在一定局限性。
分别根据算法平均时间复杂度和算法实现难度划分八大排序算法如下图
开始详细介绍排序算法之前,我想向你强烈安利一个学习数据结构与算法的神奇网站VisuAlgo http://visualgo.net。这个网站里面有各种数据结构和算法的动画展示,在教师教授或者学生自行学习相关数据结构和算法时可以十分直观的呈现算法执行过程。
**一个神奇的数据结构和算法学习网站:[VisuAlgo](http://visualgo.net)**
# 冒泡排序
算法思想:
冒泡排序是一种简单的比较排序算法。在待排序的数组中,使用双层循环遍历数组,外循环保证遍历每个元素,内循环进行比较和交换。每一遍内循环过程中,对相邻的两个数依次进行比较和交换,让较大的数往下沉(向右移动),较小的往上冒(向左移动)。
内循环不交换直接结束:如果内循环完全不交换,这意味着数组已经排序完成,我们可以在这个点上停止冒泡排序,这样可以提高算法效率。
执行样例:
输入:[29,10,14,37,14,25,10]
算法实现:
void bubbleSort(vector<int> &nums, int n){
for(int i=0;i<n;++i){
bool swapped = false;
for(int j=1;j<numsLen-i+1;++j){
if(nums[j]<nums[j-1]){
swap(nums[j],nums[j-1]);
swapped = true;
}
}
if(!swapped){
break;
}
}
}
# 直接插入排序
算法思想:
直接插入排序的主要思想就是将序列视为有序和无序两个部分,将无序部分中的元素插入到有序部分的适当位置保证仍然有序。
可以采用双层循环实现插入排序,外层循环扩展有序区间大小,内层循环用于将待排序元素插入到有序部分。
执行样例:
输入:[29,10,14,37,14,25,10]
算法实现:
void insertionSort(vector<int> &nums, int n) {
for (int i = 0; i < n; ++i) {
for (int j = i; j > 0 && nums[j] < nums[j-1]; --j) {
swap(nums[j], nums[j-1]);
}
}
}
# 简单选择排序
算法思想:
简单选择排序的核心思想就是对号入座,第一步将待排序序列中最小的元素放在数组第一个位置,以此类推始终找无序部分中最小的元素放到有序部分的末尾。
可以采用双层循环实现简单选择排序:外层循环遍历每一个待放入正确元素的位置;内层循环用于选择无序部分中最小的元素,并将该元素与外层循环位置元素交换。
执行样例:
输入:[29,10,14,37,14,25,10]
算法实现:
void selectSort(vector<int> &nums, int n){
for(int i=0;i<n-1;++i){
int min = i;
for(int j=i+1;j<n;++j){
if(nums[min]>nums[j]){
min = j;
}
}
swap(nums[i],nums[min]);
}
}
# 希尔排序
算法思想:
希尔排序是对直接插入排序的改进,又被称为缩小增量排序。该算法的核心思想是多轮分割,分别插入,将数组分割成若干个子集,然后在子集内分别使用直接插入排序;然后迭代缩小增量即分割的步长,并重复插入排序过程,直到最终数组排序完成。
实现过程中,首先以步长为 gap = length/2 把数组分割成若干个子集,然后在每个子集中进行插入排序。完成一轮分割和排序后,迭代缩小分割步长并根据缩小的步长进行下一轮分割和插入排序。直到步长缩小为 gap = 1时,则数组排序完成。
执行样例:
输入:[29,10,14,37,14,25,10]
| 步长 | 分割 | 排序 |
|---|---|---|
| gap = 7 / 2 = 3 | [29,10,14,37,14,25,10] | [10,10,14,29,14,25,37] |
| gap = 3 / 2 = 1 | [10,10,14,29,14,25,37] | [10,10,14,14,25,29,37] |
算法实现:
void shellSort(vector<int> &nums){
int length = nums.size();
int tmp;
//步长
int gap = length / 2;
while (gap > 0) {
for (int i = gap; i < length; i++) {
tmp = nums[i];
int preIndex = i - gap;
while (preIndex >= 0 && nums[preIndex] > tmp) {
nums[preIndex + gap] = nums[preIndex];
preIndex -= gap;
}
nums[preIndex + gap] = tmp;
}
gap /= 2;
}
}
# 快速排序
算法思想:
快速排序是对冒泡排序的一种改进,其核心算法思想是:使用基准将要排序的数据分割成小于基准和大于基准的两部分;然后在被分割的两个部分中递归按基准划分的步骤,最终递归到一个部分仅有一个元素组成,此时数组排序完成。
算法实现过程中,在使用快排之前可以将数组打乱,因为快排是不稳定的算法,在原数组大部分元素是有序的情况下效率提升不明显。
实现快排步骤如下:
- 先选取基准,可以以序列第一个元素作为基准
- 然后使用碰撞指针遍历数组,从指向数组尾部的指针 tail 开始移动,将数组尾部小于基准的元素覆盖到指向数组头部的指针 head;接着移动 head 找到大于基准的元素覆盖到 tail;重复该过程直到一次遍历完成,将基准值放到指针相遇位置,将数组划分为小于基准和大于基准的两部分。
- 在被分割的两部分中递归选择基准和划分序列的步骤,直到递归结束完成排序
执行样例:
输入:[29,10,37,14,25,10,14]
为了友好展示快排的效果我们稍微调整了一下之前的例子。另外更值得注意的是,受限于VisuAlgo网站动态演示创建方式,动画中并不是使用双指针遍历序列,而是直接使用冒泡排序对划分的部分进行排序。
算法实现:
void quickSort(vector<int> &nums, int l, int r) {
if (l + 1 >= r) {
return;
}
int head = l, tail = r - 1, key = nums[head];
while (head < tail){
while(head < tail && nums[tail] >= key) {
--tail;
}
nums[head] = nums[tail];
while (head < tail && nums[head] <= key) {
++head;
}
nums[tail] = nums[head];
}
nums[head] = key;
quick_sort(nums, l, head);
quick_sort(nums, head + 1, r);
}
# 堆排序
算法思想:
堆排序是对简单选择排序的改进,其核心思想是利用大根堆或者小根堆的树形结构,不断获取堆顶元素存入排序序列。大根堆是指一棵二叉树的每个节点值都大于或者等于它的左右子节点值,其根节点为最大值;小根堆反之。
实现堆排序由两个关键任务:一是要构建大根堆或者小根堆;二是在取出堆顶之后,调整堆保持大根堆或者小根堆的树形结构。
堆构建过程:堆构建有自上而下和自下而上两种方法,我们采用简单的自上而下构建
根据数组顺序插入树节点
如果插入节点值小于父节点,继续插入其他节点
如果插入节点值大于父节点,那么需要将该节点不断上浮,直到找到合适的插入位置
需要注意的是大根堆或者小根堆都是一棵完全二叉树,可以直接使用数组映射完全二叉树,不需要去另外构建树节点结构体;使用数组映射完全二叉树,索引从 0 开始具有如下性质:
当前节点的父节点索引为
(i-1)/2当前节点的左节点索引为
2*i+1当前节点的左节点索引为
2*i+2 = 2*(i+1)堆调整过程:
取出堆顶之后,用最后一个叶子节点与堆顶交换
因为最后一个叶子节点是数组的最小元素,所以将它放到大根堆堆顶,就破坏大根堆堆的树形结构,需要调整堆
选取根节点的左右节点中较大的节点与当前根节点交换
交换后如果破坏了子树的堆结构,就需要按照上述调整步骤递归地调整堆结构
执行样例:
输入:[29,10,14,37,16,25,20]
为了友好展示快排的效果我们稍微调整了一下之前的例子,删去了重复的元素
- 大根堆构建过程

- 堆排序过程
算法实现:
// 下沉调整大根堆,比较节点及其子节点,节点值大的子节点与父节点交换
void sink(vector<int> &nums, int i,int heapSize){
if(heapSize==0 || nums.empty()) return;
// 找到当前节点、左节点、右节点中较大的一个节点索引
int bigger = i;
int leftChild = 2*i+1;
if(leftChild < heapSize){
bigger = nums[leftChild] > nums[i] ? leftChild:i;
}
int rightChild = 2*i+2;
if(rightChild < heapSize){
bigger = nums[rightChild] > nums[bigger] ? rightChild:bigger;
}
// 如果较大节点是左右节点中的一个,交换当前节点和较大节点
if(bigger!=i){
swap(nums[i],nums[bigger]);
sink(nums,bigger,heapSize); // 递归调整
}
}
void buildHeap(vector<int> &nums, int heapSize){
// 从最后一个非叶子节点开始构造
int i=(heapSize-1)/2;
for(i;i>=0;--i){
sink(nums,i,heapSize);
}
}
// 递归排序时,堆根节点先与最后一个节点进行交换,交换后,堆大小减1,并对根节点进行下沉调整
void sort(vector<int> &nums, int &heapSize){
swap(nums[0], nums[heapSize - 1]);
--heapSize;
sink(nums,0,heapSize);
}
void heapSort(vector<int> &nums){
int heapSize = nums.size();
buildHeap(nums,heapSize);
for(int i=0;i<nums.size()-1;++i){
sort(nums,heapSize);
}
}
# 归并排序
算法思想:
归并排序的核心思想是采用分治策略,将整个数组的排序任务分类为两个子问题,前一半排序和后一半排序,然后整合两个有序部分完成整体排序。即把数组分为若干个子序列,直到单个元素组成一个序列,然后将各阶段得到的序列组合在一起得到最终完整排序序列。
归并排序任务可以如下分治完成:
- 把前一半排序
- 把后一半排序
- 把两半归并到一个新的有序数组,然后再拷贝回原数组,排序完成。
执行样例:
输入:[29,10,14,37,14,25,10]
算法实现:
// 将数组 a 的局部 a[s,m] 和 a[m+1,e] 合并到 tmp, 并保证 tmp 有序,然后再拷贝回 a[s,m]
void merge(vector<int>& arr, int start, int mid, int end, vector<int> tmp){
int pTmp = 0;
int pLeft = start; int pRight = mid+1;
while(pLeft<=mid&&pRight<=end){
if(arr[pLeft] < arr[pRight]){
tmp[pTmp++] = arr[pLeft++];
}else{
tmp[pTmp++] = arr[pRight++];
}
}
while(pLeft<=mid){
tmp[pTmp++] = arr[pLeft++];
}
while (pRight<=end)
{
tmp[pTmp++] = arr[pRight++];
}
for(int i=0;i<pTmp;i++){
arr[start+i] = tmp[i];
}
}
// 归并排序递归调用,先排前半部分,在排后半部分,最后将两部分结果合并
void mergeSort(vector<int>& arr, int start, int end, vector<int> tmp){
if(start < end){
int mid = start + (end-start)/2;
mergeSort(arr,start,mid,tmp);
mergeSort(arr,mid+1,end,tmp);
merge(arr,start,mid,end,tmp);
}
}
# 桶排序/基数排序
算法思想:
通排序,顾名思义就是为一个值设立一个桶,在通内记录每个值的属性,然后对桶进行排序。例如 [25,10,14,14,14,25,10],我们遍历一遍数组可以建立三个桶 [25,10,14],并将相同值的元素放到同一个桶中形成 [[25,25],[10,10],[14,14,14]];然后对三个桶进行排序 [10,14,25],然后依次输出桶中的元素完成排序。
基数排序就是进行多次桶排序,基数排序中根据进制位数字分配桶,然后根据桶的顺序收集,接着在高进制位继续迭代该过程直到最高进制位完成排序。当然,基数排序也可以根据其他属性用于其他类型的排序,核心思想都是先按低优先级分配收集排序,再按高优先级分配收集排序。
执行样例:
输入:[8,27,19,15,30,6,9]

算法实现:
void radixSort(vector<int> &nums){
// 计算最大位数
int maxOne = *max_element(nums.begin(),nums.end());
int bit = 1;
while(maxOne>=10){
maxOne /= 10;
++bit;
}
// 创建十个桶
vector<queue<int>> buckets(10);
// 多次桶排序
for(int m=0;m<bit;++m){
// 分配 一次遍历将根据对应位的数值放到对应桶中
for(int i=0;i<nums.size();++i){
int tmp = nums[i];
for(int j=0;j<m;++j){
tmp/=10;
}
buckets[tmp%10].push(nums[i]);
}
// 情况原数组内容
nums.clear();
// 收集 根据桶的顺序收集桶中的元素
for(int i=0;i<10;++i){
while(!buckets[i].empty()){
nums.push_back(buckets[i].front());
buckets[i].pop();
}
}
}
}
