02 快速排序

快速排序简介

算法思想：

快速排序是对冒泡排序的一种改进，其核心算法思想是：使用基准将要排序的数据分割成小于基准和大于基准的两部分；然后在被分割的两个部分中递归按基准划分的步骤，最终递归到一个部分仅有一个元素组成，此时数组排序完成。

算法实现过程中，在使用快排之前可以将数组打乱，因为快排是不稳定的算法，在原数组大部分元素是有序的情况下效率提升不明显。

实现快排步骤如下：

• 先选取基准，可以以序列第一个元素作为基准
• 然后使用碰撞指针遍历数组，从指向数组尾部的指针 tail 开始移动，将数组尾部小于基准的元素覆盖到指向数组头部的指针 head；接着移动 head 找到大于基准的元素覆盖到 tail；重复该过程直到一次遍历完成，将基准值放到指针相遇位置，将数组划分为小于基准和大于基准的两部分。
• 在被分割的两部分中递归选择基准和划分序列的步骤，直到递归结束完成排序

执行样例：

输入：[6,1,2,7,9,3,4,5,10,8]

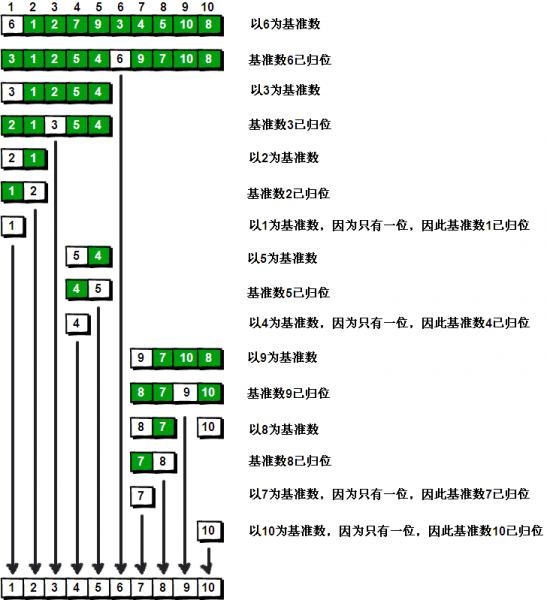
算法实现：

// 碰撞指针实现
void quickSort(vector<int> &nums, int l, int r) {
    if (l + 1 >= r) {
    	return;
    }
    int head = l, tail = r - 1, key = nums[head];
    while (head < tail){
        while(head < tail && nums[tail] >= key) {
        	--tail;
        }
        nums[head] = nums[tail];
        while (head < tail && nums[head] <= key) {
        	++head;
        }
        nums[tail] = nums[head];
    }
    nums[head] = key;
    quick_sort(nums, l, head);
    quick_sort(nums, head + 1, r);
}

// 快慢指针实现
void quickSort(vector<int> &nums, int l, int r) {
    if (l + 1 >= r) {
        return;
    }
      
    int cur = l;
    int pre = cur - 1;
    int key = nums[r-1];
      
    while (cur < r) {
        while (nums[cur] < key && ++pre != cur) {
            swap(nums[cur], nums[pre]);
        }
        cur++;
    }   
    swap(nums[++pre], nums[r-1]);
      
    quickSort(nums, l, pre);
    quickSort(nums, pre + 1, r);
}

215 数组中的第K个最大元素 (opens new window)

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

输入一个数组和一个目标值 k，输出一个整数表示第 k 大的数字。题目默认一定有解。

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

解析：

一种简单的思路就是将整个数组排完序，然后输出第 k 个最大元素。

我们可以使用快速排序的思想，减少程序的时间复杂度。根据快速排序核心思想衍生出的**快速选择一般用于求解 k-th Element 问题**，可以在 O(n) 时间复杂度，O(1) 空间复杂度完成求解工作。

快速选择的实现和快速排序相似，不过只需要找到第 k 大的枢（pivot）即可，不需要对其左右再进行排序，即在快速排序的基础上增加递归跳出条件，在找到第 k 大的枢时直接终止递归即可，减少时间复杂度。与快速排序一样，快速选择一般需要先打乱数组，否则最坏情况下时间复杂度为 O(n^2)。

class Solution {
public:
    int partation(vector<int>& nums, int k, int start, int end){
        if(start>=end) return -1;
        // 随机化处理
        int idx = start + rand() % (end - start); 
        swap(nums[start], nums[idx]);
        // 一遍遍历与交换
        int head = start, tail = end-1;
        int key = nums[head];
        while(head < tail){
            while(head<tail && nums[tail]>=key){
                --tail;
            }
            nums[head] = nums[tail];
            while(head<tail && nums[head]<=key){
                ++head;
            }
            nums[tail] = nums[head];
        }
        nums[head] = key;
        // 计算当前枢是否为第 k 大的枢
        int a = end - tail;
        // 是第 k 大的枢直接返回
        if(a==k){
            return nums[head];
        }else if(a > k){
            // 在当前枢右侧，递归快速选择
            partation(nums,k,tail+1,end);
        }else{
            // 在当前枢左侧，递归快速选择
            partation(nums,k-a,start,tail);
        }
        return nums[nums.size()-k];
    }

    int findKthLargest(vector<int>& nums, int k) {
        return partation(nums,k,0,nums.size());
    }
};